| This page has numerous bugs and omissions that are currently being worked on Wherever you see an  you can click to view a game you can click to view a game
Top Score: 619  | ||||||||||||||||||||||||
| vs Emmanuel Ede who scored 386 in FSL round 184 | ||||||||||||||||||||||||
| Best Margin: 279  | ||||||||||||||||||||||||
| 603 - 324 vs Stephen Perry in FSL round 187 | ||||||||||||||||||||||||
| Best Joint Score: 1054  | ||||||||||||||||||||||||
| 497 - 557 with Susan Edge in FSL round 194 | ||||||||||||||||||||||||
| Best CSW Word: 176 * 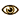 | ||||||||||||||||||||||||
| vI(N)CIBLE | ||||||||||||||||||||||||
| Best NWL Word: 102 * 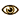 | ||||||||||||||||||||||||
| PIXI(E)iSH | ||||||||||||||||||||||||
| Best Non-Bonus CSW Word: 87 * 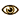 | ||||||||||||||||||||||||
| FAIX (E)X (M)I | ||||||||||||||||||||||||
| Best Non-Bonus NWL Word: 66 * 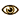 | ||||||||||||||||||||||||
| QUa(R)TZ | ||||||||||||||||||||||||
| Rob Martin was FSL tournament champion in rounds 142, 151, 158, 163, 165, 167, 168, 170, 171, 172, 181, 185, 196 & 198 | ||||||||||||||||||||||||
| Rob Martin had clean sweeps in FSL rounds 133 & 135 | ||||||||||||||||||||||||
| * Words have only recorded since round June 2019. Scores have been recorded since January 2013. |