| This page has numerous bugs and omissions that are currently being worked on Wherever you see an  you can click to view a game you can click to view a game
Top Score: 554 | ||||||||||||||||||||||||
| vs Dom Borg who scored 216 in FSL round 122 | ||||||||||||||||||||||||
| Best Margin: 338 | ||||||||||||||||||||||||
| 554 - 216 vs Dom Borg in FSL round 122 | ||||||||||||||||||||||||
| Best Joint Score: 971  | ||||||||||||||||||||||||
| 443 - 528 with Billy Smith in FSL round 185 | ||||||||||||||||||||||||
| Best CSW Word: 203 *  | ||||||||||||||||||||||||
| OXYToN(E)S | ||||||||||||||||||||||||
| Best NWL Word: 96 *  | ||||||||||||||||||||||||
| WELDERS (OUTVIE)S | ||||||||||||||||||||||||
| Best Non-Bonus CSW Word: 82 * 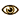 | ||||||||||||||||||||||||
| QU(OD)S (HEAP)S U(N) Q(I) | ||||||||||||||||||||||||
| Best Non-Bonus NWL Word: 76 * 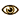 | ||||||||||||||||||||||||
| WRY(N)ECK | ||||||||||||||||||||||||
| Elliott Manley had a clean sweep in FSL FSL round 16 | ||||||||||||||||||||||||
| * Words have only recorded since round June 2019. Scores have been recorded since January 2013. |