This page has numerous bugs and omissions that are currently being worked on
Wherever you see an you can click to view a game

Elo RatingsAs at 1st Jul 2025Current period
CSW2227.0-9.8
NWLUnratednone
FrançaisUnratednone

Average Score
per Turn*		As at 1st Jul 2025Current period
CSW24.924.5
NWLUnratedNo completed games
FrançaisUnratedNo completed games
* Average Score per Turn is a time-weighted mean

Top Score: 618
vs Billy Smith who scored 264 in FSL round 249
 
Best Margin: 354
618 - 264 vs Billy Smith in FSL round 249
 
Best Joint Score: 943
445 - 498 with Andrew Duncan in FSL round 288
 
Best CSW Word: 185 *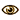
UNACtI(V)E
 
Best Non-Bonus CSW Word: 100 *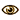
QAID I(F) A(E) Q(I)
 
* Words have only recorded since round June 2019. Scores have been recorded since January 2013.